First, listen to the
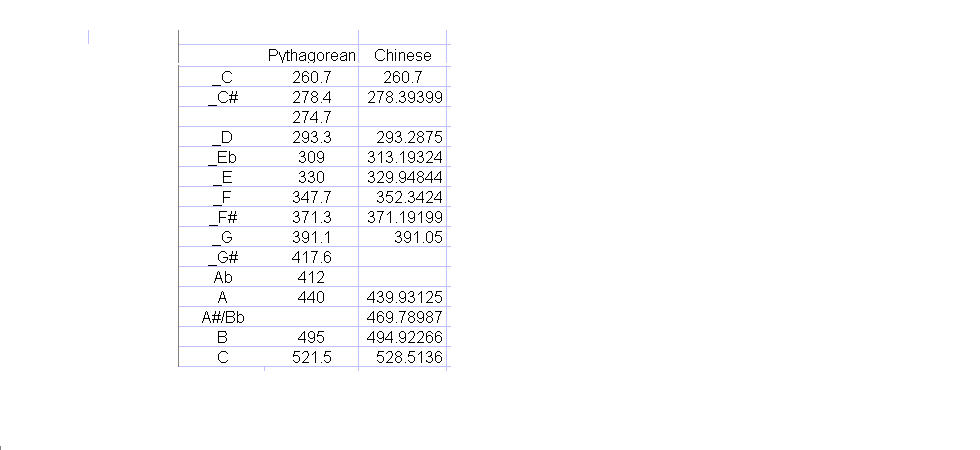
Equal Tempered tuning used to play a scale. This is the scale you will hear on a properly tuned piano.
Now, listen to one of the many
Chinese tunings used to play a similar scale. Unless you have perfect pitch, you might not be able to tell the difference without a better
musical context. Later on in this discussion, you will be given an opportunity to hear identical melodies played in Equal Tempered and Chinese 12 Lyu tunings.
(By "tuning" I mean a rule that one uses to determine how to tune the strings of an instrument such as a harp so that it will play the
frequencies that it is supposed to play.) Because of the notes coming in a musical sequence, and because frequently several notes are played
at the same time, you will be better able to hear the differences among the various tunings.
Before we can talk about the Chinese musical scales, it may be helpful to review some things about our own music and what we consider to be harmonious. The original Chinese musical theory was probably developed by making rules for the lengths of a set of bamboo tubes that were made to be blown, perhaps in the way that people now blow over the ends of bottles to make a musical note. It will be easier to explain things in terms of stringed instruments.
Let's start with a long narrow piece of wood that is over a meter long. At the left end (unshown) we will put tuning pegs, and at the right end we will put a resonating chamber. But for right now we are just concerned with what will be analogous to the long neck of a guitar with its frets. The vibrating part of our strings will be 100 cm. long.

The easiest way to get harmonious singing is for everyone to sing the same note. But people sing in different registers, some high and some low. We say that they are singing the same note, but actually the frequencies they sing are found by doubling some fundamental frequency, doubling it again, and so on. We say that these people are singing an octave, or octaves, apart.
Let's put a metal fret at the midpoint of the actively vibrating part of our string. If you halve the length of a string (and don't change its tension), then you double its frequency.

If we were actually to build this instrument, we could provide several strings. We could set them all to C=260, stop one string with our finger at the middle fret, and play that one and an unstopped string together. We would hear frequencies of 260 hertz and 520 hertz together. We could even add another fret a quarter of the way from the right end, giving us 1040 hertz.

If we multiply the fundamental frequency (in this case 260 hertz) by an even number we will find that the high frequency waves fit exactly within the envelope created by the fundamental frequency. To human being, and apparently to many of our animal friends, such sounds are more pleasant. To experience a counter-example, try striking two adjacent keys on a piano, or playing two adjacent holes on a harmonica. Or, try listening to this recording of two guitar strings tuned so as to produce an unpleasant interaction.
An unpleasant chord.
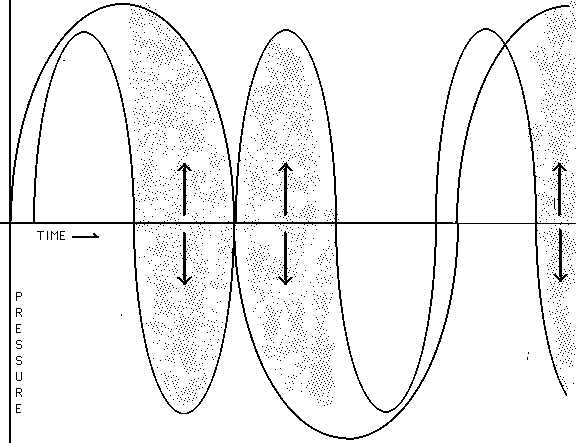
When two sound waves interfere, part of the time they augment each other, but part of the time one sound wave is trying to do the opposite of the other sound wave. The result is that the sound you hear comes and goes very rapidly. You will hear a kind of "wah, wah, wah, wah, wah" as a result. If you have a piano available, you can try various combinations for yourself. Playing four notes together, A, A an octave higher, F, and F an octave higher may produce some interesting results. You can also listen to a "wav" file below. This example gives the high F first, to demonstrate the highest note that is actually played in the second part. When the second part comes on, you may be able to hear two interesting things. There is a "wah-wah" fluctuation that occurs about every half second, and has a low, buzzy quality. There is also a high frequency tone, an octave higher than the single reference tone at the beginning of the recording that has a pronounced warble.
Hear the high "ghost" instrument.
In the graph drawn below, the grayed-in areas are the parts where the two sound waves interfere. You would hear the sound "drop out" at this point.
We don't want an irritating fire siren type sound. So let's add a second fret that will give us harmony. We started with 100 cm. divided by 1. 100 cm. / 1 = 100 cm. Then we put down one fret in the middle. That's 100 cm./2 = 50 cm. and it gave us the octave. Now we will try 100 cm./3 = 33.33...3 cm. But putting a fret there would be too near the right end of the string. It would be an octave higher than we want. So we will double that length (making it an octave lower than it was). Then we have (100 cm. /3)*2=66.66...6
We found out by experiment that halving the length of a string doubles its frequency. The general relationship is given by the equation:
L1/L2 = F2/F1 so F2= (L1/L2)*F1.
100/50 = F2/260 so F2=(100/50)*260=2*260=520
and similarly
100/66.66...6=F2/260 so F2=(100/66.66...6)*260=((100*3)/(2*100))*260=3*130=390
In this scale, 390 hertz is E.

We can't get any good out of dividing our string by four because that amounts to multiplying our fundamental frequency by four, and that is a few octaves above our fundamental frequency.
So let's try 5. Following the mathematical steps shown above, that will give us a fret at the 80 cm. mark (20 cm. from the tuning pegs), and a frequency of 325, which is C#.

The next multiple of the fundamental frequency we could try is 7. That gives us a frequency of 455 hertz and tells us to set a fret so that we can use a string length of about 57.1 cm. That will give us a G.

9 is the next multiplier, and it yields a frequency of 292.5 hertz and a string length of about 88.9 cm. That's a B.

10 won't help, so we must use 11. That yields 72.72...72 cm and 357.5 hertz for an D#.

13 yields a string length of about 61.5 cm. and a frequency of 422.5 hertz. That's an F#.

15 yields a string 53 1/3 cm. long and a frequency of 487.5, a G#.

Finally, a change of routine. 17 doesn't sound nice, and we have to go all the way to 21 to find values for D. The string length is about 76.2 and the frequency is 341.25 hertz.

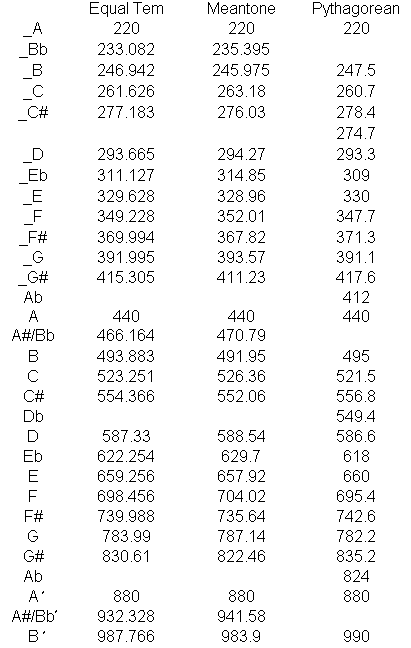
There are a few sharps and flats missing, but rather than trying the method of multiplication used above so other methods were used. There are also differences in methods for calculating D and F# that cause discrepancies of around 10 hertz. Our purpose here is not to be exhaustive, but to produce a correct gamut of one kind to which the Chinese system may be compared.
For a chart showing the calculations and including the values of D and F# associated with the system of just intonation created by Ptolemy and Mersenne, click here.
Now let's here the diatonic scale (the one that goes "do, re, mi...") in that tuning. (click here)
If you have perfect pitch, or even just perfect relative pitch, you may have been troubled by the feeling that certain notes on various musical instruments sound out of tune. And yet, all the musical instruments have the same frequencies. It's not the fault of your ears. It's because we play a tempered scale -- a scale that slightly detunes certain notes so that when a piece of music is transposed to another key it still sounds to us as though it is in key.
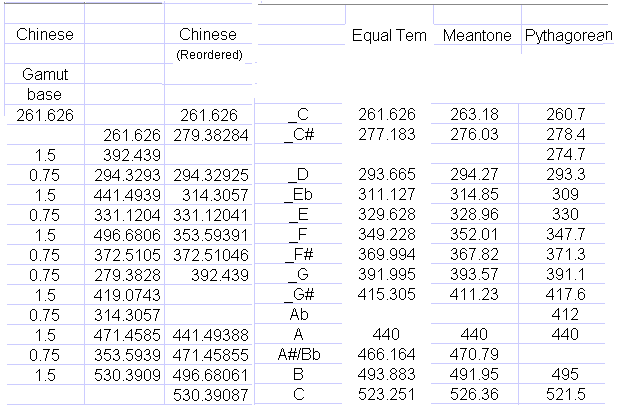
Tables at the end of this article will show differences that cause problems when transposing keys in untempered scales, and they will also show how the Chinese gamut of frequencies differs from an untempered Western scale and the tempered Western scale.
Now let's put down frets according to the Chinese method. This method has an ancient history, and was first written about in the Lyu Shi Chun-qiu, a text produced by the "think tank" of a late Zhou dynasty figure around 239 B.C., and the Guan Zi, a syncretic text attributed to a very early figure, Guan Zhong, who died in 644 B.C. The book may have been compiled in the late fourth century B.C., but may also contain materials going back to the historical Guan Zhong's time.
The Chinese rule is very simple: Take 2/3 of the length of the open string, and put down a fret there. Then take 4/3 of that second length and put down a fret there. The third step is to take 2/3 of the last length, then 4/3, and so forth. Let's see how that works.
The first step is to put down a fret that will leave 2/3 of
the whole string free to vibrate. If the open string is tuned
to 260 hertz, then stopping a fret at the 2/3 mark will provide
390 hertz.

The second step is to put a fret at a point 4/3 of the stopped
length of the string just determined. That fret will provide
292.5 hertz.



Step five uses 2/3 and provides about 493.6 hertz.

Step six uses 4/3 and provides about 370.2 hertz.

Step seven uses 4/3 because using 2/3 would create
a sound an octave too high. It provides about 277.6 hertz.

Step eight uses 2/3 and provides about 416.5 hertz.

Step nine uses 4/3 and provides about 312.4 hertz,

Step ten uses 2/3 and provides about 468.5 hertz.

Step eleven uses 4/3 and provides about 351.4 hertz.

Step twelve uses 2/3 and provides about 527.1 hertz. Note that
the true octave is at 520 hertz. Using this system would never
permit derivation of the true octave. But the method used here
continually divides frequencies by two (or multiplies string lengths
by two) to make a gamut all the notes of which fall within one octave,
so it is clear that the early Chinese had a clear idea of how to define
and use the octave. The values derived in this twelfth step are not
used in normal musical practice.

The following is a comparison of the fret placement by the Chinese method (the lower set of frets) and by the Western method detailed above.

On the other hand, if a musician has an instrument like the bagpipe that is not very much like other instruments, then the only thing to do is to learn what can be done with that instrument that is musically interesting and pleasing. And any gamut that can be produced will present a different set of possibilities and difficulties.
Traditional Chinese music uses a gamut of frequencies that are guaranteed to provide some level of discord in certain combinations that would sound more harmonious in the western musical tuning described above or even in the Equal Tempered tuning. But sometimes people like a little discord for the sake of spice, and a piece of music that is composed with the Chinese system in mind can sound more brilliant and endearing than the same piece played in the Equal Tempered tuning -- because most notes in that system are deliberately flatted as a way to provide a compromise tuning that will tolerate transposition from one key to another.
Most of us grow up using the tempered scale which you can produce for yourself on any well-tuned piano. But that scale is mathematically rather sophisticated. (It involves complications involving the twelfth root of two.) Before that scale was invented, some less sophisticated scales were produced. Two of them are shown for comparison in the chart below.
One of the reasons for inventing mathematically defined scales was to facilitate the creation of musical instruments that permit transposing from key to key. The advantage is that one can play in many keys without having many sets of musical instruments or constantly retuning one set of instruments. The disadvantage is that they are all compromises. They are all slightly out of tune and produce some degree of discord.
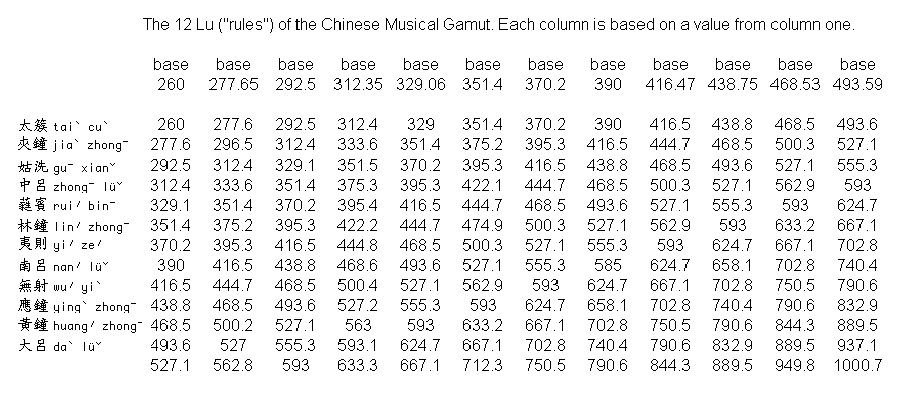
The Chinese system is based on the mathematical method of working back and forth by taking 3/2 of a base frequency, 3/4 of the frequency so produced, and so forth. Once a series of 12 frequencies is produced, they use each of those 12 frequencies as the fundamental frequency for a new scale. The result is 144 frequencies. (It turns out that there are quite a few duplications.) That gives the Chinese musician quite a large set of frequencies to play music with.
If the musical intervals between notes were exactly equal, then the numbers along any diagonal that rises from left to right should be the same. But, in fact, the intervals are not equal, and the numbers along those diagonals are not always equal.
Note that the bottom line turns out not to be a true octave above the top line. Each of the numbers calculated is somewhat higher than the octave.
When children in the U.S. "learn to sing the scale", they learn what is technically called a "major diatonic scale." It consists of 8 notes, do, re, mi, fa, sol, la, ti, and back to do. Adjacent keys on a piano are a semitone apart in pitch. From do to re is a full tone, from re to mi is a full tone, but from mi to fa is a semitone. Then fa to so, so to la, and la to ti are all full tones, but ti to do is another semitone. So in English and American practice, at least, you can start a scale with C, and it will look like this: C, D, E, F, G, A, B, C. And you can just as easily start from C# and get an other scale: C#, D#, F, F#, G#, A#, C, C#. Actually, most people will not know whether they are singing a song in one or the other key unless someone starts them out with a pitch pipe. It is the sequence of tones and semitones that is crucial. There is also a minor diatonic scale, in which the sequence of tones and semitones is scrambled, but most people do not know exactly what that sequence is -- even though they may recognize a song in a minor key when they hear it.
Chinese music uses not one or two but five basic scales. They are pentatonic scales. You can get an idea of what one of these scales would sound like by composing and playing a song that could be performed by using only the black keys of the piano. The five choices of frequency intervals are color coded in the chart below. In traditional Chinese music, both the frequency intervals (gong, shang, jue, zhi, or yu) and the fundamental frequency for a scale could be specified. That has been shown by constructing one of each of the five choices of frequency intervals on a randomly chosen fundamental frequency, and those choices have also been color coded. (The Chinese also had heptatonic scales, but they were not used as often as were the pentatonic scales.)
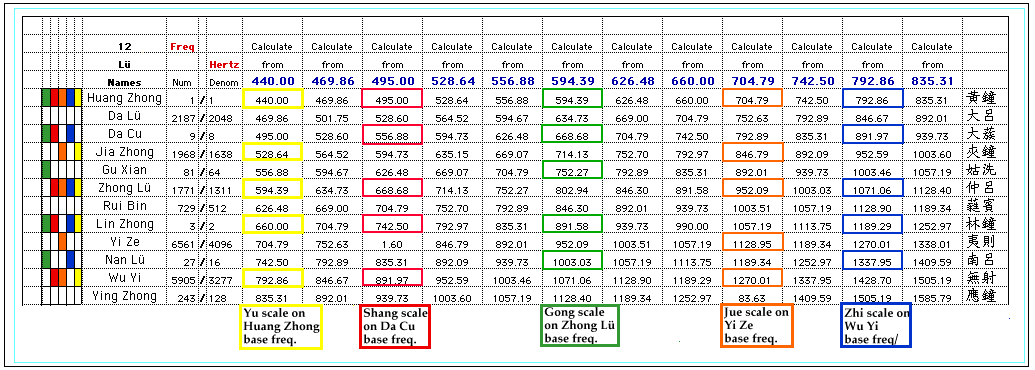

1/1 same
2187/2048 vs. 256/243
9/8 same
1968/1638 vs. 32/27
81/64 same
1771/1331 vs. 4/3
729/512 same
3/2 same
6561/4096 vs. 128/81
27/16 same
5905/3277 vs. 16/9
243/128 same