E 2558. Proposed by A. Torchinsky, Cornell University
Suppose that ![]() is a divergent series of positive terms, and let
is a divergent series of positive terms, and let
![]() for
for ![]() . For which values of p
does the series
. For which values of p
does the series ![]() converge?
converge?
Solution by Elmer K. Hayashi. We prove a more general theorem from which we
deduce
that ![]() converges if and only if p>1.
converges if and only if p>1.
Theorem. Let f(x), for x>0, be any nonnegative, continuous,
monotonically decreasing,
real-valued function. If ![]() is a divergent series of positive terms
and if
is a divergent series of positive terms
and if
![]() for
for ![]() , then
, then
and
Proof: Intuitively we reason that if u=sn then du is analogous to
sn - sn-1=an. Hence ![]() probably behaves somewhat like
probably behaves somewhat like
![]() . Furthermore, if F(x) is any antiderivative of the continuous
function f(x), then
. Furthermore, if F(x) is any antiderivative of the continuous
function f(x), then ![]() . Thus a
natural series with which to compare
. Thus a
natural series with which to compare ![]() is the telescoping series
is the telescoping series
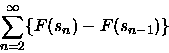 |
(1) |
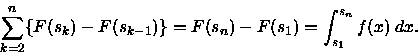 |
(2) |
From equation (2), it is apparent that the series (1) converges if and only
if the integral,
![]() , is convergent. Now, by the mean value theorem,
, is convergent. Now, by the mean value theorem,
for some ck between sk-1 and sk. Since f is monotonically
decreasing, we
have for ![]() ,
,
and
Using the Comparison test, we arrive at the conclusion of the theorem.
If we take ![]() , we conclude that
, we conclude that ![]() converges for p > 1 and
converges for p > 1 and ![]() diverges for
diverges for ![]() .
In general, it is not true that if
.
In general, it is not true that if ![]() is diverent, then
is diverent, then
![]() is also divergent. For
example, if
is also divergent. For
example, if ![]() , a1 = s1 = 1 + e and
an = sn-1 exp (2n-1)
for n > 1, then
, a1 = s1 = 1 + e and
an = sn-1 exp (2n-1)
for n > 1, then ![]() . The series
. The series ![]() is
divergent, by our theorem, since
is
divergent, by our theorem, since ![]() is
divergent. However
is
divergent. However
![]() behaves like
behaves like ![]() and therefore is convergent.
However, in the
special case
and therefore is convergent.
However, in the
special case ![]() , it is true that
, it is true that
![]() does diverge.
does diverge.
It suffices to prove ![]() diverges since
diverges since ![]() for all sufficiently large n if
for all sufficiently large n if ![]() as
as
![]() and
and ![]() . By the comparison test, the
divergence of
. By the comparison test, the
divergence of
![]() would
then imply the divergence of
would
then imply the divergence of ![]() for all
for all ![]() . There are
two cases to consider. Either
. There are
two cases to consider. Either ![]() for all sufficiently large
n or otherwise there exist infinitely many n such that an > sn-1.
In the former case, we have for all sufficiently large n
for all sufficiently large
n or otherwise there exist infinitely many n such that an > sn-1.
In the former case, we have for all sufficiently large n
But we know ![]() is divergent, and hence, by the comparison
test,
is divergent, and hence, by the comparison
test,
![]() is also divergent. In the second case, we have for
infinitely many
n
is also divergent. In the second case, we have for
infinitely many
n
Thus ![]() and
and ![]() is divergent in this
case, too. This completes our proof.
is divergent in this
case, too. This completes our proof.
Elmer K. Hayashi Department of Mathematics Wake Forest University Winston-Salem, N. C. 27109